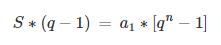Princípio da indução finita

Definição e exemplos do princípio da indução finita

Este princípio é utilizado para a solução de diversos exercícios, porém ele serve apenas para aqueles que envolvem números inteiros e para exercícios que pedem que seja provado que algo é verdadeiro para um conjunto de valores inteiros.

Vou falar sobre o princípio utilizando a fórmula da soma da PA (Progressão Aritmética) para esclarecer.

 

Para isso, será necessário o uso da fórmula do termo geral da PA:

Voltamos ao método, que basicamente consiste em 3 etapas:

1ª Etapa - Dado um conjunto de valores inteiros que se deseja verificar a validade de algo proposto, deve-se verificar se é válido para o menor valor do conjunto.

No exemplo então, vamos verificar se a fórmula da soma da PA é válida para n = 1. Neste caso, é muito fácil perceber já que a soma será igual a a1, já que este é o único termo.

Vamos verificar se usando a fórmula o resultado é obtido:

O resultado obtido é correto, logo a fórmula da Soma da PA vale para o menor elemento do conjunto.

2ª Etapa - Assume-se que para um elemento 'k' qualquer e genérico do conjunto a fórmula é verdadeira.

Do exemplo vamos calcular a soma dos primeiros 'k' elementos do conjunto, neste caso, pela fórmula da soma da PA teremos que:

3ª Etapa - Assumindo que o resultado obtido na Etapa 2 seja verdadeiro, calculamos o resultado para 'k+1' e verificamos se obtemos a fórmula desejada.

Do exemplo usado temos então que a soma dos 'k+1' primeiros elementos é a soma dos 'k' primeiros elementos mais o elemento 'k+1'. Veja:

Observe que se usarmos a fórmula da soma da PA para calcular a soma dos 'k+1' primeiros termos (substituindo n = k+1) teremos exatamente o resultado acima. Portanto, provamos que a fórmula é válida sempre. Porém, por que podemos concluir isso? Por que o uso do princípio garante a validade da fórmula para qualquer quantidade de elementos?

Bom, tudo se resume às etapas que foram seguidas. 

Foi mostrado que para o primeiro elemento a fórmula é válida. 

Após isso, supomos na Etapa 2 que para um número de elementos 'k' qualquer ela é válida e a partir do resultado da Etapa 2 obtemos o resultado para 'k+1' e verificamos que ele é válido. A grande dúvida que surge é por que podemos garantir que o resultado obtido na Etapa 2 é válido?

Na verdade a gente não garante isso, apenas supõe. Porém se a partir do resultado da Etapa 2 pudermos obter um resultado satisfatório na Etapa 3 então o resultado é válido. O que garante isso é o seguinte raciocínio:

- Para o menor elemento a equação é válida;

- Então, se 'k' = 1 a nossa suposição da Etapa 2 é verdadeira, e não apenas uma suposição, já que mostramos na Etapa 1 isso;

- Mas na Etapa 3 nós mostramos que se 'k' é verdadeiro, então 'k+1' também é;

- Como para 'k' = 1 vimos que é verdadeiro na Etapa 1, então certamente para 'k+1' = 2 também será, como visto na Etapa 3;

- Mas se para 'k' = 2 é verdadeiro, então para 'k+1' = 3 também será;

- Mas se para 'k' = 3 é verdadeiro, então para 'k+1' = 4 também será;

- ...

Assim, o princípio garante que para qualquer 'k' ele é verdadeiro, desde que as etapas sejam satisfeitas.

Exercícios que o princípio foi usado:

Somatório de n²

Dedução da fórmula da soma da PG por indução

Aula sobre PG

Exercício Resolvido - Somatório de N² = 1² + 2² + 3² + ... + n² ou ∑(n^2) = 1^2 + 2^2 + 3^2 + ... + n^2

Ache uma equação para calcular o somatório de N² = 1² + 2² + 3² + ... + n², sendo n um número inteiro.

Solução:

O cálculo de ∑n² pode ser feito de várias formas. Tentarei demonstrar algumas:

1º método:

Sabendo que:

(n+1)³ - n³ = (n³ + 3n² + 3n + 1) - n³ = 3n² + 3n + 1

Assim:

∑[(p+1)³ - p³] = ∑[3p² + 3p + 1]

Mas:

∑[(p+1)³ - p³] = (2³ - 1³) + (3³ - 2³) + ... + [(n+1)³ - n³]

Perceba que o primeiro termo de cada parênteses é cancelado com o segundo do parênteses seguinte, sobrando apenas:

(n+1)³ - 1³

Então:

(n+1)³ - 1 = ∑[3p² + 3p + 1]

Mas:

∑[3p² + 3p + 1] = ∑3p² + ∑3p + ∑1 = 3*∑p² + 3*∑p + (1+1+1+1+1+...+1)

∑p = 1 + 2 + 3 + 4 + .. + n  -> (PA)

∑p = (1+n)*(n/2)

Temos também que:

∑1 = n

Assim:

(n+1)³ - 1 = ∑[3p² + 3p + 1]

(n+1)³ - 1 = 3*∑p² + 3*(1+n)*(n/2) + n

n³ + 3n² + 3n = 3*∑p² + 3n/2 + 3n²/2 + n

3*∑p² = n³ + 3n²/2 + n/2

∑p² = (1/6)*[2n³ + 3n² + n] = (1/6)*n*(n+1)*(2n+1)

2º método:

Usando o triângulo de Pascal:

Imagem retirada do livro Algorithmic Information heory, de G. Chaitin

Como o que queremos é o somatório:

1 + 4 + 9 + 16 + ... + n²

Se observarmos no triângulo acima a terceira coluna, o primeiro termo dela (1), é 1², se somarmos o primeiro ao segundo, temos 1+3 = 4, se somarmos o segundo ao terceiro, temos 3+6 = 9, o terceiro ao quarto 6+10 = 16 ....

Ou seja, a soma dois a dois dos termos da coluna, formam exatamente os termos da sequência que queremos:

Assim:

Ou, agrupado de forma melhor:

Mas, pelo teorema das colunas, que diz que:

Temos:

e

Tendo, por fim:

1² + 2² + 3² + 4² + ... + n² = (1/6)*n*(n+1)*(n-1 + n+2) = (1/6)*n*(n+1)*(2n+1)

3º método:

Digamos que a gente já conheça o resultado, mas desejamos provar que ele vale pelo método da indução finita :

Se n = 1:

1² = (1/6)*1*(1+1)*(2+1) = 1 Ok, é válido

Agora, a gente supõe que para n = k-1, a fórmula também é válida, admitimos então que:

1² + 2² + 3² + ... + (k-1)² = (1/6)*(k-1)*[(k-1)+1]*[2(k-1)+1] = (1/6)*(k-1)*k*(2k-1)

Supondo que a fórmula acima seja correta, devemos provar que vale para n = k também:

1² + 2² + 3² + 4² + ... + (k-1)² + k² = [(1/6)*(k-1)*k*(2k-1)] + k²

1² + 2² + 3² + 4² + ... + (k-1)² + k² = [(1/6)*(k²-k)*(2k-1)] + k²

1² + 2² + 3² + 4² + ... + (k-1)² + k² = [(1/6)*(2k³ - k² - 2k² + k)] + k²

Fazendo o mínimo múltiplo comum, ou seja, transformando k² = (6/6)*k² temos:

1² + 2² + 3² + 4² + ... + (k-1)² + k² = (1/6)*(2k³ - 3k² + k + 6k²) =

1² + 2² + 3² + 4² + ... + (k-1)² + k² = (1/6)*(2k³ + 3k² + k)

1² + 2² + 3² + 4² + ... + (k-1)² + k² = (1/6)*k*(k+1)*(2k+1)

que é a fórmula (1/6)*n*(n+1)*(2n+1) para n = k. Logo, esta provado por indução.

Dedução da fórmula da soma da PG por indução.

Fórmula da soma da PG (Progressão Geométrica) - DEDUÇÃO

Uma PG é definida por um termo inicial (a1) e uma razão (q). Cada termo desta sequência é o anterior multiplicado da razão, assim a sequência fica:

A soma dos termos de uma Progressão Geométrica nada mais é do que:

1 - Utilizando o método da indução finita para calcular a Soma da PG:

Provaremos que a Soma da PG é dada por:

1º) Veremos se a fórmula é válida para n = 1:

O que é verdadeiro, já que o resultado da Soma de uma Progressão Geométrica com apenas um termo é ele mesmo.

2º) Supomos que a fórmula da Soma da PG é válida para um valor "n" aleatório:

3º) Partindo da hipótese assumida acima, devemos chegar que a fórmula da Soma da PG é válida para "n+1":

A soma "S(n+1)" será a soma de todos os termos da PG até n (Sn) mais o termo a1*q^(n), tendo assim:

Porém, pela suposição assumida em 2º, temos:

Que pode ser escrito como:

Logo, a fórmula da Soma da PG é verdadeira.

Outra forma de deduzir a fórmula da Soma da PG

Agora, para aplicar o método, multiplicamos a Soma da PG por 'q', tendo:

Agora fazemos a seguinte subtração:

Perceba que vários dos termos serão anulados por serem iguais, restando apenas:

isolando os termos: