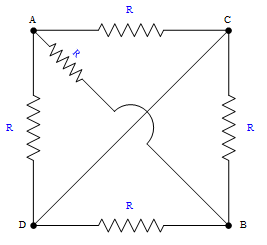
Calcule a resistência equivalente da associação mista de resistores entre os pontos A e B no circuito abaixo:
Circuito 5
Solução:
Inicialmente, é importante dar nomes aos pontos:Verificamos que há um curto entre os pontos C e D. Como já comentado nos outros casos, a melhor forma de visualizar a disposição dos resistores é unindo os pontos ligados por curto. Neste caso, os pontos C e D tornam-se um ponto só. Assim, dispomos os pontos no "espaço" e vamos unindo-os com o que houver entre eles, da seguinte forma:
Entre os pontos A e B há uma resistência;
Entre os pontos A e C há uma resistência;
Entre os ponto A e D há uma resistência;
Entre os pontos C e B há uma resistência;
E, finalmente, entre os pontos D e B há uma resistência;
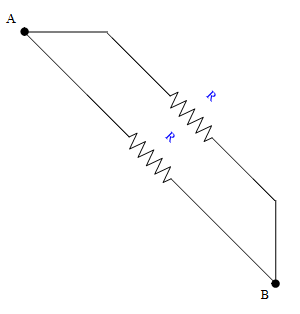
Agora fica fácil visualizar o circuito, que deve ser resolvido iniciando pelos resistores em paralelo.
Como devemos calcular a resistência equivalente entre A e B, temos que os resistores R/2 estão em série (neste momento o ponto C//D pode ser eliminado).
Restando dois resistores em paralelo. Assim, a resistência equivalente entre A e B é R/2.


















O circuito da resposta está diferente do circuito proposto.
ResponderExcluirRossini Terra, obrigado pela mensagem. Corrigido já.
ExcluirGrande abraço.
faltou a unidade no Req
ResponderExcluirObrigado pelo comentário Matheus. Porém, nesses exercícios, como a resistência não é um valor numérico, não há necessidade de colocar a unidade, subintende-se que R contém a unidade.
ExcluirCara, parabens. Simplesmente adorei o site/explicações. Mas meu caso eh um pouco pior: nele nao existe o resistor entre A e B,mas existe um entre C e D. Como devo proceder? Desde ja muito obrigado.
ResponderExcluirNa verdade seu caso é mais simples. Se não existe o resistor entre A e B, então o ponto C e D está em curto, logo os resistores CB e BD estão em paralelo, assim como os resistores AD e AC.
ExcluirExplicação excelente.
ResponderExcluir