Exercício Resolvido - Geometria analítica (Ponto e Reta)

Determinar a projeção ortogonal do ponto P(2,4) sobre a reta.

x = 1+2t

y = -1+3t

Solução:
Vou fazer a solução deste exercício de duas formas. Uma envolvendo apenas conhecimentos de geometria analítica básica (mais trabalhosa), outra envolvendo conceitos vetoriais.

Método 1:
Inicialmente vou determinar a reta na forma y = a.x + b. Para isso, basta isolar o 't' nas duas igualdades acima:

x = 1 + 2t
t = (x - 1) / 2

y = -1 + 3t
t = (y + 1) / 3

(x - 1) / 2 = (y + 1) / 3
3x - 3 = 2y + 2
2y = 3x - 5
y = 1,5x - 2,5

sabe-se que retas ortogonais tem o produto dos seus coeficientes angulares igual a -1.
Logo, a reta ortogonal à reta acima, da forma:
y = ax + b
Será tal que:

a*(1,5) = -1
a = -2/3
Porém essa reta passa pelo ponto (2,4)
y = (-2/3)x + b
4 = (-2/3).2 + b
b = 4 + 4/3
b = 16/3

Logo, a reta que é ortogonal à y = 1,5x - 2,5 e passa por P(2,4) é: y = (-2/3)x + 16/3
Assim, a projeção ortogonal do ponto P na reta y = 1,5x - 2,5 será a intersecção dessas duas retas, e a intersecção ocorre quando temos os valores de y e x iguais, logo:

1,5x - 2,5 = (-2/3)x + 16/3
x(3/2 + 2/3) = 5/2 + 16/3
x(9/6 + 4/6) = 15/6 + 32/6
x(13/6) = 47/6
x = 47/13

Logo, o ponto será:
(47/13 , 38/13)

Método 2: 

Utilizando teoria vetorial
x = 1+2t
y = -1+3t
Esta reta tem a forma vetorial:
(x,y) = (1,-1) + t*(2,3)
O vetor diretor da reta é (2,3)

Logo, uma reta ortogonal a essa terá vetor diretor ortogonal a (2,3). Se eles são ortogonais e diferentes de zero, o produto escalar entre eles será zero.

Assim:
(a,b).(2,3) = 2a + 3b = 0

Arbitrando a = 1, b = -2/3. Como o valor de 'a' pode ser arbitrado e ele é diretamente proporcional a 'b', se utilizarmos a = 3, b = -2. Apenas para trabalharmos com números inteiros.

Logo, sabendo que esta reta passa pelo ponto (2,4), a reta será:
(x,y) = (2,4) + h*(3, -2)
ou
x = 2 + 3h
y = 4 - 2h

Achando o ponto de intersecção das retas:
2 + 3h = 1 + 2t -> h = (-1 + 2t) / 3
4 - 2h = -1 + 3t
4 - 2*(2t - 1) / 3 = -1 + 3t
4 - 4t/3 + 2/3 = -1 + 3t
17/3 = 13t/3
t = 17/13

Logo, x = 47/13 e y = 38/13

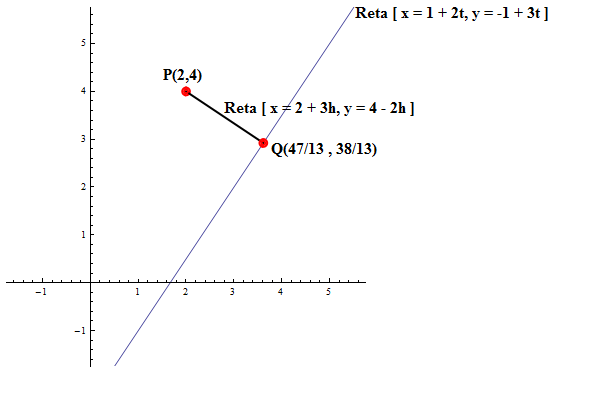
Gráfico do exercício abaixo: