Fórmula da soma da PG (Progressão Geométrica) - DEDUÇÃO
Uma PG é definida por um termo inicial (a1) e uma razão (q). Cada termo desta sequência é o anterior multiplicado da razão, assim a sequência fica:
A soma dos termos de uma Progressão Geométrica nada mais é do que:
Provaremos que a Soma da PG é dada por:
1º) Veremos se a fórmula é válida para n = 1:O que é verdadeiro, já que o resultado da Soma de uma Progressão Geométrica com apenas um termo é ele mesmo.
2º) Supomos que a fórmula da Soma da PG é válida para um valor "n" aleatório:
3º) Partindo da hipótese assumida acima, devemos chegar que a fórmula da Soma da PG é válida para "n+1":
A soma "S(n+1)" será a soma de todos os termos da PG até n (Sn) mais o termo a1*q^(n), tendo assim:
Porém, pela suposição assumida em 2º, temos:
Outra forma de deduzir a fórmula da Soma da PG
Agora, para aplicar o método, multiplicamos a Soma da PG por 'q', tendo:
Agora fazemos a seguinte subtração:

Perceba que vários dos termos serão anulados por serem iguais, restando apenas:

isolando os termos:
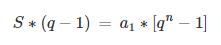


















Muito boa!!!
ResponderExcluirObrigado pelo comentário.
ExcluirMuito boa!!!
ResponderExcluirObrigado pelo comentário.
ExcluirAjudou bastante, conseguir compreender
ResponderExcluir